友情提示:同学您好,此页面仅供预览,在此页面学习不会被统计哦! 请进入学习空间后选择课程学习。
●对统计理论的诘难
力学可逆性 vs 热学不可逆性
Loschmidt的质疑:根据力学定律的时间可逆性,分子体系热运动的逆向运动也是允许的。而这导致熵减!

逆状态的出现需要等待很长时间(甚至超过宇宙年龄!),即便出现了也只是一瞬间
宇宙“热寂”说:宇宙的熵终将达到极大值,即宇宙将最终达到热平衡
现今对宇宙的理解——1.宇宙在膨胀;2.宇宙作为自引力系统,是具有负热容的不稳定系统
宇宙是不稳定的热力学系统,并不像静态宇宙模型所设想的那样具有平衡态,因而其熵亦无最大值
●各态历经假说(ergodic hypothesis)
Boltzmann认为,孤立系统从任意初态出发,足够长时间后将经历一切可能的微观状态
企图把统计规律性还原为力学规律性
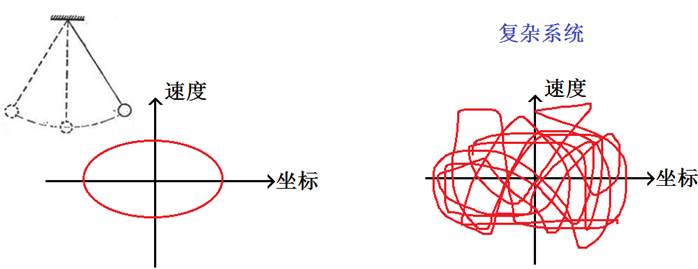
1930年,Birkhoff运用现代数学工具测度论证明,孤立系统经历足够长时间后可无限接近初态 等概率假设的基础
Gibbs系综理论:用系综来考查系统,比Maxwell和Boltzmann更具普遍性
● Gibbs佯谬
|
| 同种分子,把隔板抽掉,所有分子微观状态数变2倍,体系熵增加?! 不可能
全同粒子的量子性 |