友情提示：同学您好，此页面仅供预览，在此页面学习不会被统计哦！ 请进入学习空间后选择课程学习。
●最小作用量原理
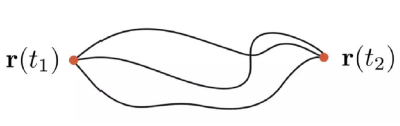
指定初始位置和最终位置，在众多路径中，粒子究竟选哪一条？
下面来做一件“奇怪的事情”：
式子并没有写错，是减号！ 积分号里的动能减势能称作拉格朗日量
·哪一条路径的作用量取极值？
如何计算？ 泛函：“函数的函数”
将某条特定路径表示为
（想想在山上跑步，沿哪条路线跑，什么时间跑到哪里？）。具体来说，就是每个时刻对应一个位置
……
此处的轨迹不一定是物理上真实的，而是人为“设计”的
无数多条轨迹中，哪条轨迹作用量最小？
微积分中，极值——一阶导数为零
但这里变化的不是一个变量，而是一个函数！
改变某条轨迹的“设计”，作微小挪动，t时刻
改变了
速度的改变为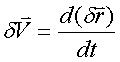
，
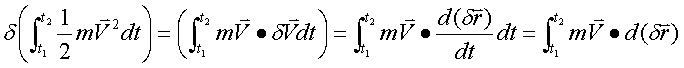分步积分，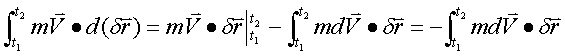
t1、t2为初始、末了时间，
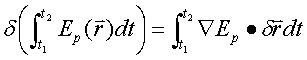
作用量的变分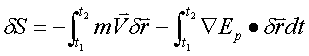
作用量取极值的路径应有
，此时
，即
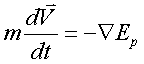得到了牛顿定律！
2017年，哥伦比亚大学的Janna Levin教授提出“什么样的科学术语或概念更应该广为人知”？——最小作用量原理