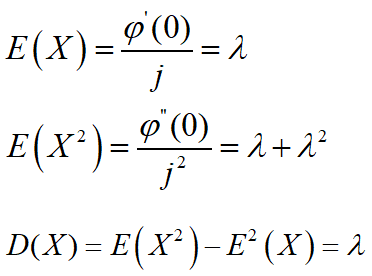随机变量的数字特征

摘要：本节回顾随机变量的均值、方差、协方差等数字特征，并讲解特征函数

随机变量的数字特征

随机变量的分布函数、概率密度和分布律等都可完整描述随机变量，但在某些实际或者理论问题中，人们更感兴趣的是某些能描述随机变量某一特征的常数。

    这种由随机变量的分布所确定的、能刻画随机变量某一方面的特征的常数统称为数字特征，在理论和实际应用中都很重要。这些重要的数字特征有：数学期望、方差、相关系数和矩。

随机变量的数学期望(均值)

    设离散型随机变量X的分布律为

若级数

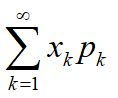
绝对收敛，则称上式为X的数学期望(均值)，记为E(X)，即

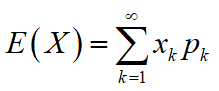
    设连续型随机变量X的概率密度为f(x),若积分

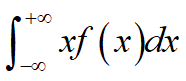
绝对收敛，则称其为X的数学期望(均值)，记为E(X)，即

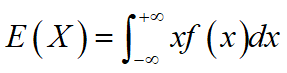
例12：设X~π(λ),求E(X)

    解:

        由于

            ，

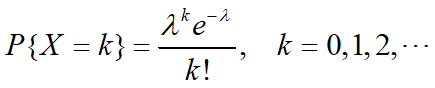      故

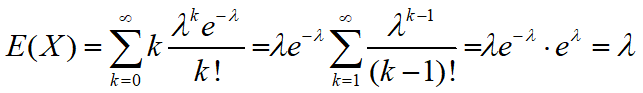
例13：设X~U(a,b),求E(X)

解:

        由于

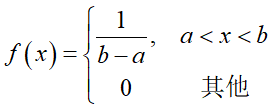
      则

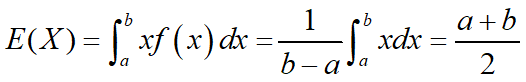
方差

设X是一个随机变量，若E{[X-E(X)]2}存在，则称其为X的方差，记为D(X)或Var(X)，即

而记 为标准差或者均方差。

    方差可计算如下：

例14：设X~π(λ),求D(X)

解:     

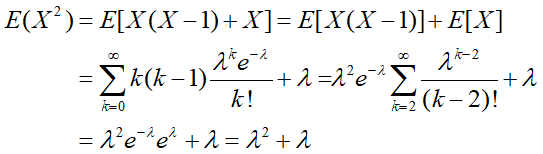
故

可见，泊松分布的均值和方差相等，都等于λ。

例15：设X~U(a,b),求D(X)

解:  

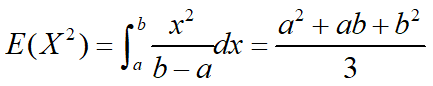
故

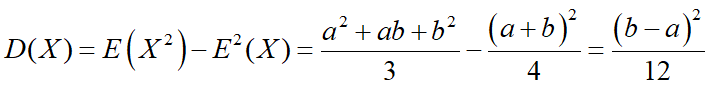
协方差和相关系数

定义如下的量：

称为随机变量X和Y的协方差，记为Cov(X,Y)。而

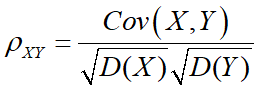
称为X和Y的相关系数。    

    下述关系成立：

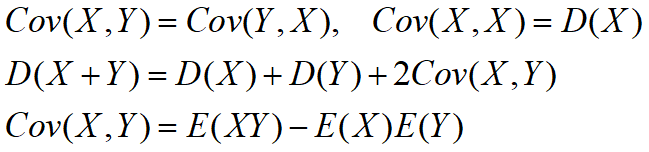
相关系数的意义

    相关系数ρXY表征了X,Y之间的线性关系紧密程度，当|ρXY|较大时，说X和Y线性相关程度较好，反之说X和Y线性相关程度较差，当ρXY =0时，称X,Y不相关。

独立和不相关

    当X和Y相互独立时，由于Cov(X,Y)=0,即X和Y不相关。因此可知 独立一定不相关。但是，不相关并不一定独立。

对于正态分布随机变量来说，不相关和独立等价。

随机变量的矩

定义：设X和Y是随机变量，如果下列量存在

则分别称为X的k阶原点矩，简称k阶矩；X的k阶中心距；X和Y的k+l阶混合矩；X和Y的k+l阶混合中心矩。

    显然,X的数学期望E(X)是X的一阶原点矩，方差D(X)是X的二阶中心距，协方差Cov(X,Y)是X和Y的二阶混合中心距。

协方差矩阵

   设n维随机变量(X1,X2,…,Xn)的二阶混合中心距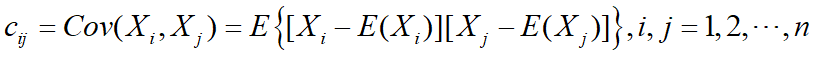

都存在，则称矩阵

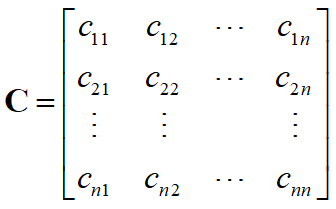
为n维随机变量(X1,X2,…,Xn)的协方差矩阵，该矩阵是一个对称矩阵。

随机变量的特征函数

    随机变量的分布函数是其概率分布的完整描述，但是分布函数一般不具有连续性、可微性等良好的分析性质，这给应用分布函数研究随机变量带来困难。而随机变量的特征函数则能与其分布函数一一对应，既能完整描述随机变量的概率分布，又具有良好的分析特性。

定义：设X是实随机变量，其分布函数为F(X)，则称

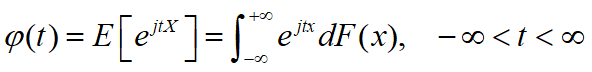
为随机变量X的特征函数。

   当X为离散型随机变量且分布律为

则特征函数为

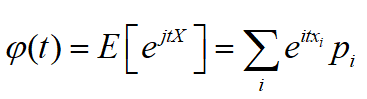
    当X为连续型随机变量且概率密度函数为f(x)，则特征函数为

例16：设X服从参数为λ的泊松分布，求其特征函数

依照定义有

例17：设X服从区间[a,b]上的均匀分布，求其特征函数

根据定义有

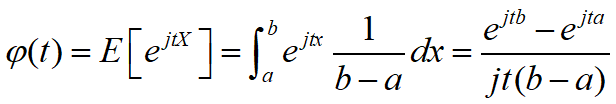
例18：设X服从正态分布N(μ,σ2)，求其特征函数

根据定义有

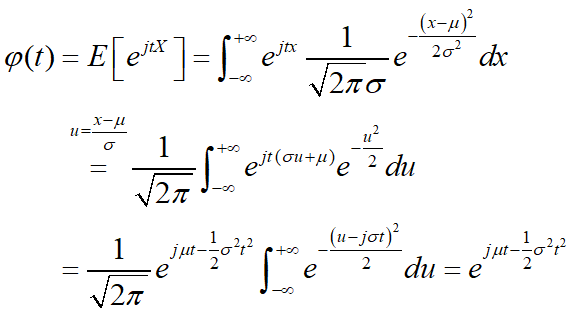
特征函数的2条重要性质

    特征函数具有多条性质，其中2条应用较多，如下：

    (1)设随机变量X,Y相互独立，又Z=X+Y，则Z的特征函数φZ(t)=φX(t)φY(t),即两个相互独立的随机变量之和的特征函数等于各自特征函数的乘积。

    (2) 设随机变量X的n阶原点矩存在，则其特征函数φ(t)存在k(k≤n)阶倒数，且φk(0)=jkE(Xk)

    利用上述性质(2)可方便地求解随机变量X的各阶矩

例18：设X~π(λ),求E(X),E(X2),D(X)

思路：可直接求解，也可使用特征函数根据上述性质(2)求解

        X为泊松分布，其特征函数为

于是：

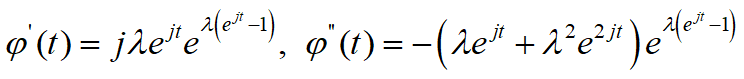
故：