概率论基础

摘要：本节课将讲解概率论基础知识，并引入贝叶斯公式、全概率公式等。

概率论与数理统计中，关于随机变量的诸多分析，都可自然地过渡到对于随机信号的分析当中，因此将概率论的相关内容作为本课程的预备知识。

确定性现象和随机现象

    在一定条件下必然发生的现象；如同性电荷相互排斥

随机现象

在相同条件下，个别试验的结果呈现不确定性，但大量重复试验的结果又呈现统计规律性；如抛硬币，炮弹落点等

随机试验

    随机现象的随机性，是通过大量重复试验而体现出来的。这种试验称为随机试验，其具有如下特点：

    1）可在相同条件下重复进行；

    2）每次试验的可能结果不止一个，能够事先明确试验的所有可能结果；

    3）进行一次试验之前不能确定哪一个结果出现；

  如抛硬币

    1）条件相同；

    2）结果可能正面也可能反面

    3）一次试验前不能确定结果是正面还是反面

样本空间、随机事件

    在随机试验中，试验的结果不止一个，称随机试验中每一种可能的结果为一个样本点，由全体样本点组成的集合称为随机试验E的样本空间，用S表示。

    一般地，称试验E的样本空间S的子集为E的随机事件，简称事件。

    不包含任何样本点的事件（空集）称为不可能事件，用Ø表示．

    在每次试验中总发生的事件称为必然事件．样本空间S本身是必然事件。

频率与概率

    一个事件（除必然事件与不可能事件外）在一次试验中可能发生，也可能不发生，其发生的可能性可用概率来描述，而概率可由频率引出。

频率：设在N次重复试验中，事件A发生nA次，则称nA为事件A发生的频数，称nA /N为事件A发生的频率

概率(统计定义)：当试验次数N增大时，事件A发生的频率nA /N将稳定于某个常数p，则称p为事件A发生的概率，记为P(A）

概率(公理化定义）：

    设E是随机试验，S是其样本空间，对S中的每一个事件A，赋予一个实数，记为P(A)，称为事件A的概率，如果集合函数P(*)满足下述三个公理：

(1) P(A)≥0;  

(2) P(S)=1; 

(3) 若事件A1,A2,…两两互不相容，则

                P(A1∪A2 ∪…)=P(A1)+P(A2)+…

概率的性质

性质1：对于任一事件A，P(A) ≤１．

性质2：(有限可加性）　设事件A1，A2，…，Am互不相容，则

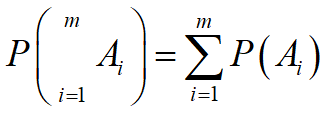
性质3：

性质4：若 ，则 

性质5：若 ，则

性质6(加法公式)：对任意两个事件A,B，有

概率示例

例1：一个小组由高矮不同的10人组成，任意地按先后顺序站成一排，试求恰好按高矮顺序排成队形的概率

思路：任意排列的结果有多种，每一个可能的结果都是样本空间的样本点，而恰好按高矮顺序排成队形这一事件是样本空间的子集，只需求出这一事件所包含的样本点个数以及样本空间的样本点总数，其比值就是所求概率。

样本空间的样本点个数？该事件包含的样本点个数？

例2：在1~2000的整数中随机地取一个数，该整数即不能被６整除，又不能被８整除的概率是多少

思路：找出不能被6整除的数字和不能被8整除的数字，统计总数，除以2000即可。该方法直接但操作复杂，此时往往利用事件运算，降低求解难度。

令事件A和B分别为“取到数字能被6整除”和“取到数字能被8整除”，于是所求概率为

条件概率

    条件概率是在已知某事件A发生的条件下，事件B发生的概率。定义如下：

    设A,B是两个随机事件，且P(A)>0 ,则称

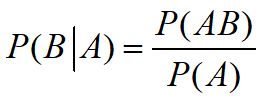
为事件A发生条件下事件B发生的条件概率。

    条件概率具有和概率同样的性质，即前述概率的6个性质，同样适用于条件概率。

条件概率示例：

    例3：设产品20件，其中有15件一等品，5件二等品，一二等品混放，现随机取两件，每次取一件，共两次，不放回抽样，求在第一次取到正品的条件下第二次仍取到正品的概率．

思路：按照条件概率的定义，求出第一次取出正品的概率，再求出前两次都取出正品的概率，用后者除以前者即得所求条件概率。

令A表示“第一次取到正品”，B表示“第二次取到正品”，则所求概率为

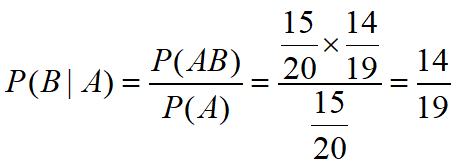
全概率公式和贝叶斯公式

概率计算中的两个非常重要的公式

样本空间的划分：

设S是试验E的样本空间，B1,B2，…,Bn是E的一组事件，若这些事件满足：

（1）

  (2) 

则称B1,B2，…,Bn为空间的一个划分或是一个完备事件组。

设试验E的样本空间为S，B1,B2,…,Bn为S的一个划分，A为S的一个事件，且

,

则全概率公式为：

贝叶斯公式为：           

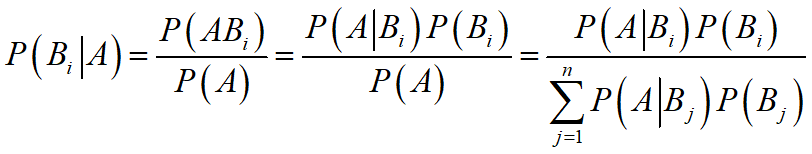
例4：某厂使用来自甲乙丙3个产地的同型号电子元件，其中来自3个产地的元件数量各占24％，30％，46％，且它们的合格率分别为94％，96％，98％，

    (1) 若任取一元件，取到的是合格品的概率是多少？

    (2) 若某一元件不合格，该其最有可能来自何产地？

思路：原件来自甲乙丙三产地这三个事件，构成了产地空间的一个划分；可借助全概率公式和贝叶斯公式解题

    令， ，分别表示元件来自甲乙丙三地，A表示元件合格，则有

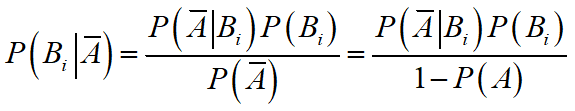
例5：已知某高炮击中飞机发动机、机舱及其他部位的概率分别为0.1,0.08, 0.39，对应的使飞机坠落的概率分别是0.95,0.89, 0.51。现高炮任意击发一次，求(1)飞机坠落的概率；(2)现已知飞机被击落，求高炮击中发动机的概率．

思路：击中发动机、机舱、其他部位和未击中这四个事件，构成了击中位置空间的一个划分；可借助全概率公式和贝叶斯公式解题

     令B1-B4分别表示击中发动机、机舱、其他部位和未击中，A表示飞机坠落，则：

独立性

    设A,B是试验E的两个事件，若P(A)>0,则可定义P(B|A)，一般来说A的发生与否对B的发生与否会有影响，即P(B|A)≠P(B)。但当P(B|A)=P(B)时，可知A发生与否与B的发生没有关系，此时说A,B是相互独立的随机事件，此时有P(AB)=P(A)P(B)。

    还可推广到多个相互独立的随机事件，如事件A,B,C,D,E相互独立，则有：                          P(ABCDE)=P(A)P(B)P(C)P(D)P(E)