二维随机变量及其分布

摘要：本节回顾二维随机变量的定义和以及连续、离散随机变量的分布

二维随机变量

    设S为随机试验E的样本空间，X,Y是定义在S上的随机变量，则称向量(X,Y)为二维随机变量。二维随机变量可看做平面上随机点的坐标。

    可用二维随机变量的分布函数描述对其统计特性.

设(X,Y)是二维随机变量，对任意实数x,y,称函数

为二维随机变量(X,Y)的分布函数，或称为随机变量X和Y的联合分布函数。

二维离散型随机变量及其分布律

如果二维随机变量(X,Y)可能的取值为有限对或者可列无限对，则称(X,Y)为二维离散随机变量并称                                           

为二维离散随机变量(X,Y)的分布律，或随机变量X和Y的联合分布律

例9：设有5件产品，正次品分别为2件和3件，现任取２次，每次取１件，取出后放回．设X是第1次取得次品的件数，Y是第2次取得次品的件数．求(X,Y)的联合分布律．

解： (X,Y)的所有可能取值(0,0) (0,1) (1,0),(1,1)

二维连续型随机变量及其分布函数

    设二维随机变量(X,Y)的分布函数为F(x,y),若存在非负函数f(x,y),使得对于任意实数x,y,都有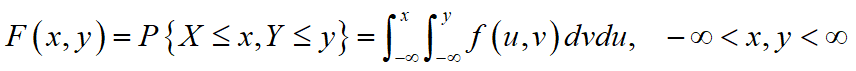

则称(X,Y)为二维连续型随机变量，称函数f(x,y)为二维连续型随机变量(X,Y)的概率密度，或称为随机变量X和Y的联合概率密

度。

例10：设二维随机变量(X,Y)具有概率密度

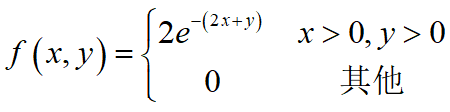
求(1) 分布函数F(x,y)

    (2) 概率P(Y≤X)

思路：对于(1)，按照分布函数定义求解即可

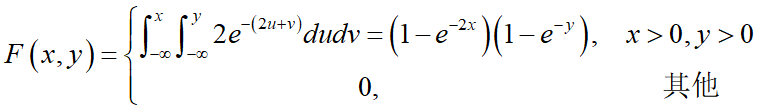
     对于(2)，确定事件Y≤X在二维平面上所占的区域，然  后在此区域对分布函数积分即可。事件Y≤X在二维平面上的区域如下，

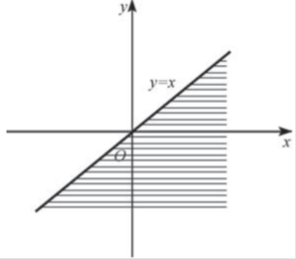
于是：

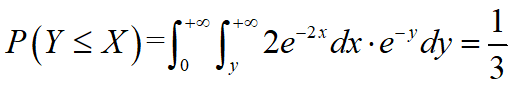
二维随机变量的边缘分布

    设(X,Y)是二维随机变量，称分量X的分布为(X,Y)关于X的边缘分布，称分量Y的分布为(X,Y)关于Y的边缘分布，分别记为FX(x)和FY(y)。边缘分布可由(X,Y)的分布函数确定：

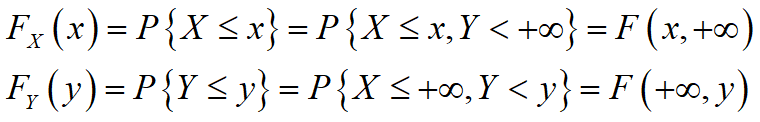
    对离散型二维随机变量(X,Y)，有

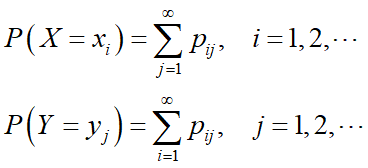
分别为X和Y的边缘分布律。

对连续型二维随机变量(X,Y)，有

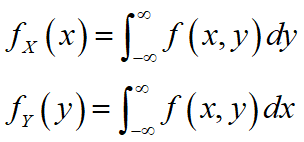
分别为X和Y的边缘概率密度。

    若对于二维随机变量(X,Y)有F(x,y)=FX(x)FY(y)，则称随机变量X和Y相互独立。此时对于离散型随机变量有

对于连续型随机变量有

二维随机变量函数的分布

    考察二维随机变量(X,Y)通过两个二元函数，生成两个新的二维随机变量(Z,Θ)的情况，求解(Z,Θ)的分布。

定理：若连续型二维随机变量(X,Y)和两个函数z=g1(x,y)及θ=g2(x,y)满足：

(1) 存在唯一的反函数x=h1(z,θ)和y=h2(z,θ)

(2) g1(x,y)、g2(x,y)、 h1(z,θ)及h2(z,θ)都是连续的

(3)    存在且连续，令

则二维随机变量(Z,Θ)的概率密度函数为：

其中定义的J 被称为雅克比因子。

例11：设(X,Y)为二维随机变量，其中X,Y相互独立且都服从正态分布N(0,σ2)，记Z为(X,Y)的模，Θ为(X,Y)的辐角，求(Z，Θ)的联合概率密度函数即边缘概率密度函数。

思路：按照上述定理，首先找出随机变量Z和Θ与二维随机变量X和Y的函数关系，判断其是否满足上述定理的条件，如果满足，则求解雅克比因子，继而求解(Z，Θ)的联合概率密度函数，最后再由联合概率密度函数求解边缘概率密度函数。

由于X,Y独立同分布，且都服从正态分布，则

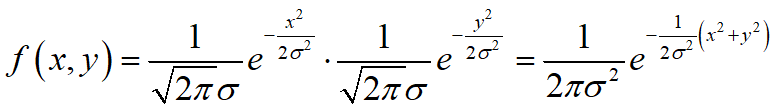
而Z和Θ与X和Y的函数关系(z=g1(x,y)及θ=g2(x,y))为

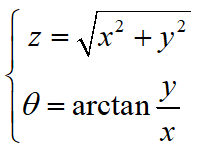
上述方程组有唯一解(反函数x=h1(z,θ)和y=h2(z,θ))

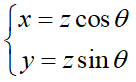
于是雅克比因子为

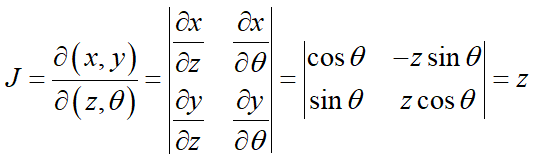
于是有：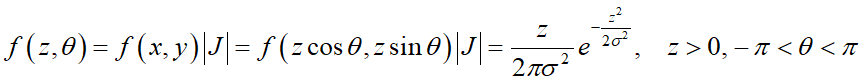

故(Z,Θ)的概率密度函数为：

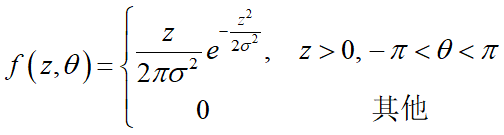
两个边缘分布为：

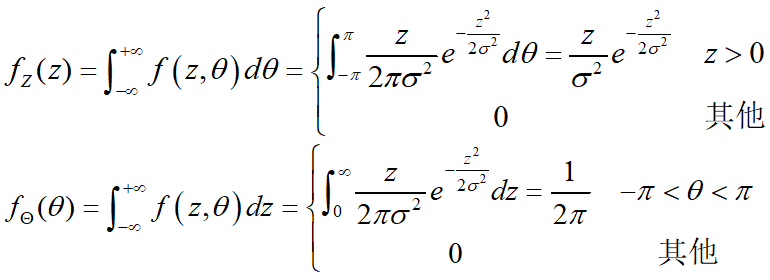
    从Z和Θ的概率密度函数可见，Z服从参数为σ的Rayleigh分布，而Θ服从区间(-π,π)上的均匀分布，并且由于

故Z和Θ相互独立。

    上述结果是工程上的一个重要结论：若二维随机变量的两个分量是相互独立且服从正态分布N(0,σ2)的随机变量，则该二维随机变量的模和辐角也是相互独立的随机变量，且模服从参数为σ的Rayleigh分布，辐角服从区间(-π,π)上的均匀分布。

    该结论可用于本课程后文所述的窄带随机过程的学习中。

    上文基于雅克比式的随机变量函数的分布的求解方法也可用于本课程的后续内容学习中。