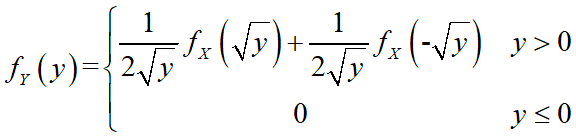随机变量及其分布
摘要:本节回顾随机变量的定义和以及连续、离散随机变量的分布
随机变量
实际问题中,随机试验的结果可能直接表现为一个数值,有些试验结果不直接表现为一个数值,但可人为地将实验结果用数值表示,于是所有的实验结果都可以和实数对应起来。这就产生了随机变量的概念。
设S是随机试验E的样本空间,对于S中的每一个样本点s,都有一个确定的实数X(s)与之对应,这样就得到在S上定义的一个单值函数X=X(s),称其为随机变量。
随机变量示例
1) 在掷硬币试验中,掷出正面记为1分,掷出反面记为0分.如果用X表示掷一次硬币的得分,则X是一个随机变量
2) 将一枚硬币抛掷3次,若令X表示出现正面的次数,那么出现3次正面的试验结果对应着随机变量X=3,其概率为P(X=3)=P{出现3次正面}=1/8
离散型随机变量及其分布律
离散型随机变量是指该随机变量的所有可能的取值是有限个或可列无穷多个。
分布律:
设X是一个离散型随机变量,它所有可能的取值为x1,x2,…(有限个或可列无穷多个),则
![]()
称为随机变量X的分布律.
分布律表征了两方面信息:随机变量的取值,和该取值对应的概率。
例6:通往目的地的道路上有四组独立的信号灯,每组以1/2概率允许或禁止汽车通过,以X表示汽车首次停下时已经经过的信号灯组数,求X的分布律
思路:汽车可能一路畅行到目的地才停下;也可能首次停在任意一组信号灯处。所有可能的情况种类是有限的,可用离散随机变量的分布律来描述
令p为单个灯允许汽车通过的概率(此例为1/2),则分布律为
| X | 0 | 1 | 2 | 3 | 4 |
| pi | 1-p | p(1-p) | p2(1-p) | p3(1-p) | p4 |
常见的离散型随机变量分布律
1)0-1分布
若随机变量X的分布律为:
![]()
则称其服从0-1分布(也称两点分布或伯努利分布) 。该分布亦可表示为:
| X | 0 | 1 |
| pi | 1-p | p |
对于某一随机试验,若其样本空间S中只有2个元素,这种试验称为伯努利试验,此时总可将这两个元素分别对应于0和1,从而构成定义在S上的0-1分布。
2)二项分布
将伯努利试验独立重复进行n次,则这一串重复的独立试验称为n重伯努利试验。令A为伯努利试验中的某事件,且P(A)=p,若以X表示n重伯努利试验中事件A出现的次数,则X的分布律为:
![]()
称此分布为二项分布。
二项分布就是描述n重伯努利分布中事件A发生次数的概率分布,当n=1时,二项分布就成为0-1分布。
3)泊松分布
若随机变量X的分布律为
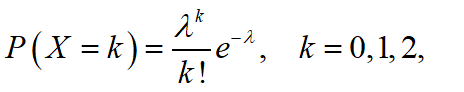
则称X服从参数为λ的泊松分布。
泊松分布有着广泛的应用,例如某段时间内电话机收到的呼唤次数、一本书一页中的印刷错误数、某地区在一天内邮递遗失的信件数、某天到达某商店购买某种商品的顾客人等都服从泊松分布。
随机变量的分布函数
很多时候,人们所感兴趣的并不是随机变量取某个值的概率,而更感兴趣的是取值位于某个区间的概率,此时就要用到分布函数。
对于某随机变量X和任意实数x,{X≤x}是一个事件,因此对应一定的概率P(X≤x),此概率是x的函数,由此可定义随机变量的分布函数如下:
设X是一个随机变量,则
![]()
称为X的分布函数。
例7:设X的分布律如下,求其分布函数
| X | 3 | 4 | 5 |
| pi | 0.1 | 0.3 | 0.6 |
思路:由于X的取值是离散的,因此分布函数要分几种情况进行求解。
当x<3时, P(X≤x)=0; 当3≤x<4时,P(X≤x)=0.1;
当4≤x<5时,P(X≤x)=0.4;当5≤x时, P(X≤x)=1;
于是
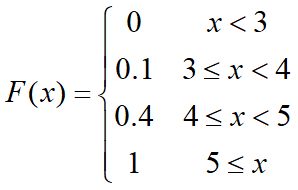
连续性随机变量及其概率密度函数
离散型随机变量的统计规律性可用分布律来描述.而连续型随机变量的取值不能一一列举出来,其取值常常充满一个区间或几个区间,因而研究它在每一点处取值的概率没有意义。此时可用概率密度函数来表征其统计规律性。
设随机变量X的分布函数为F(x),如果存在非负函数f(x),使得对于任意实数x,有
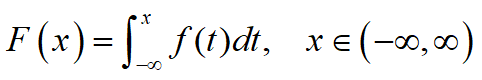
则称X为连续性随机变量,称f(x)为其概率密度函数
需要注意的两点:
1) 连续型随机变量X取任一给定值a的概率为0;
证明:取∆x,则有0≤P(X=a)≤P(a-∆x<X≤a),而
P(a-∆x<X≤a)=F(a)-F(a-∆x)
当∆x→0时上式为0,于是0≤P(X=a)≤0,即P(X=a)=0
2) 虽然P(X=a)=0,但并不意味着X=a是不可能事件。也就是说,概率为0的事件不一定是不可能事件,但反过来,不可能事件的概率必为0
例8:设随机变量X的概率密度为
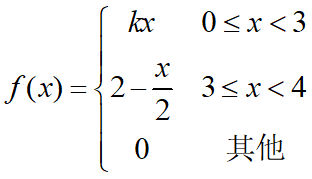
(1)确定常数k
(2)求X的分布函数
(3)求P{1<X≤7/2}
思路: 利用f(x)在(-∞, ∞)积分等于1,可求k;根据分布函数的定义,可求分布函数;将X取值范围下界、上界带入分布函数并求差值可得(3)。
(1) k=1/6 ;
(2)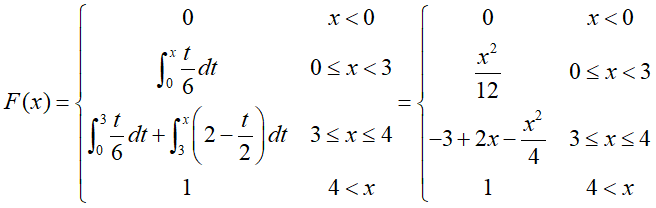
(3) 41/48
常见的连续型随机变量
1) 均匀分布 若随机变量X具有概率密度
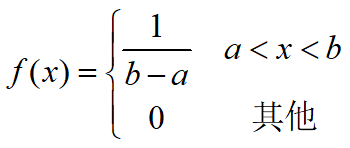
则称X服从均匀分布.
2) 指数分布 若随机变量X具有概率密度
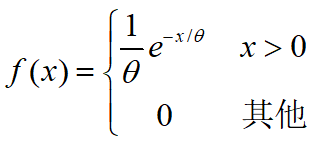
则称X服从指数分布.
许多“等待时间”以及半导体元件寿命等都可用指数分布来描述,因此其在排队论和可靠性理论中应用广泛。
3) 正态分布
若随机变量X具有概率密度
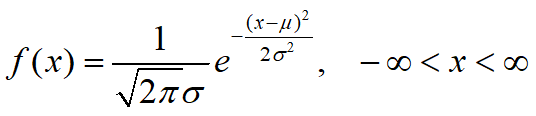
则称X服从均值为μ,方差为σ2的正态分布.
在自然或社会现象中,大量随机变量都服从或近似服从正态分布.如班级学生身高、某零件的尺寸等都服从正态分布.在理论研究和实际应用中服从正态分布的随机变量起着特别重要的作用.
随机变量函数的分布
随机变量是试验结果的函数,会随着试验结果的变化而变化,而随机变量的函数也会随着试验结果的变化而变化,因而也是一个随机变量.
同样地,随机变量的函数可以是离散型随机变量,也可以是连续型随机变量,其统计特性可分别用分布律和概率密度函数表示。
前者求解较为简单,后者求解稍微复杂一点。
(1) 离散型随机变量函数的分布(例示)

求Y=2X+1和Y=(X-2)2的分布律
解:
求出与X各取值对应的Y值,并与相应概率对应即可
Y=2X+1
| Y | 1 | 3 | 5 | 7 | 9 | 11 |
| pk | 1/12 | 1/6 | 1/3 | 1/12 | 2/9 | 1/9 |
Y=(X-2)2
| Y | 0 | 1 | 4 | 9 |
| pk | 1/3 | 1/4 | 11/36 | 1/9 |
(2) 连续型随机变量函数的分布(例示)
设随机变量X的概率密度如下,求Y=2X+8的概率密度
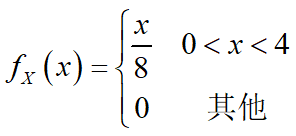
思路:连续性随机变量函数的分布,应通过分布函数来求解
令FX(x)和FY(y)分别为X和Y的分布函数,则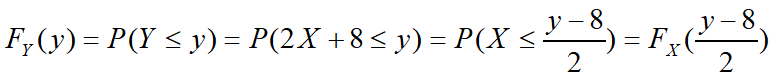
两边对y求导得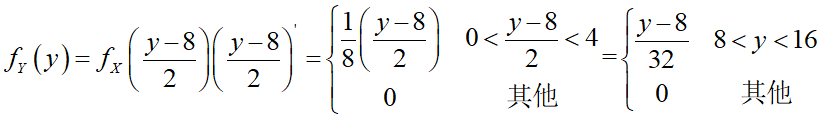
设随机变量X的概率密度为fX(x),(-∞<x< ∞),求Y=X2的概率密度
思路:依旧按照前述方法使用分布函数求解
由于Y=X2≥0,故y≤0时,FY(y)=0;当y>0时,
![]()
故

因此,Y的概率密度为