检索结果共
个
5.1
低通滤波器的理论基础
5.1.1
集总元件低通滤波器
5.1.2
阶梯阻抗低通滤波器
5.1.3
短截线低通滤波器
5.1.4
带通和带阻滤波器的理论基础
5.2
集总参数低通滤波器的设计
5.3
微带线阶梯阻抗低通滤波器的设计
5.4
微带短截线低通滤波器的设计
5.5
集总参数带通滤波器的设计
5.6
平行耦合微带线带通滤波器设计
10
友情提示:同学您好,此页面仅供预览,在此页面学习不会被统计哦! 请进入学习空间后选择课程学习。
可以将集总元件低通滤波器变换为分布参数低通滤波器,分布参数低通滤波器采用微带短截线实现。其中,理查德(Richards)变换用于将集总元件变换为传输线,科洛达(Kuroda)规则可以将各滤波器元件分隔开。
1.理查德(Richards)变换
通过理查德(Richards)变换,可以将集总元件的电感和电容用一段终端短路或终端开路的传输线等效。终端短路和终端开路传输线的输入阻抗具有纯电抗性,利用传输线的这一特性,可以实现集总元件到分布参数元件的变换。
终端短路的一段传输线可以等效为集总元件电感。当传输线的长度l=λ0/8时,等效关系为
jXL= jωL=JZ0tan(π/4*Ω)=SZ0 (5.7)
式(5.7)中 S=jtan(π/4*f/f0) (5.8)
同样,终端开路的一段传输线可以等效为集总元件电容。当传输线的长度为l=λ0/8时,等效关系为
jBC= jωC=JY0tan(π/4*Ω)=SY0 (5.9)
2.科洛达(Kuroda)规则
科洛达(Kuroda)规则是利用附加的传输线,得到在实际上更容易实现的滤波器。例如,利用科洛达规则既可以将串联短截线变换为并联短截线,又可以将短截线在物理上分开。在科洛达规则中附加的传输线称为单位元件,当f=f0时这段传输线长为λ/8 。科洛达(Kuroda)规则包含4个恒等关系,如图5.3所示,图中的电感和电容分别代表短路和开路短截线。
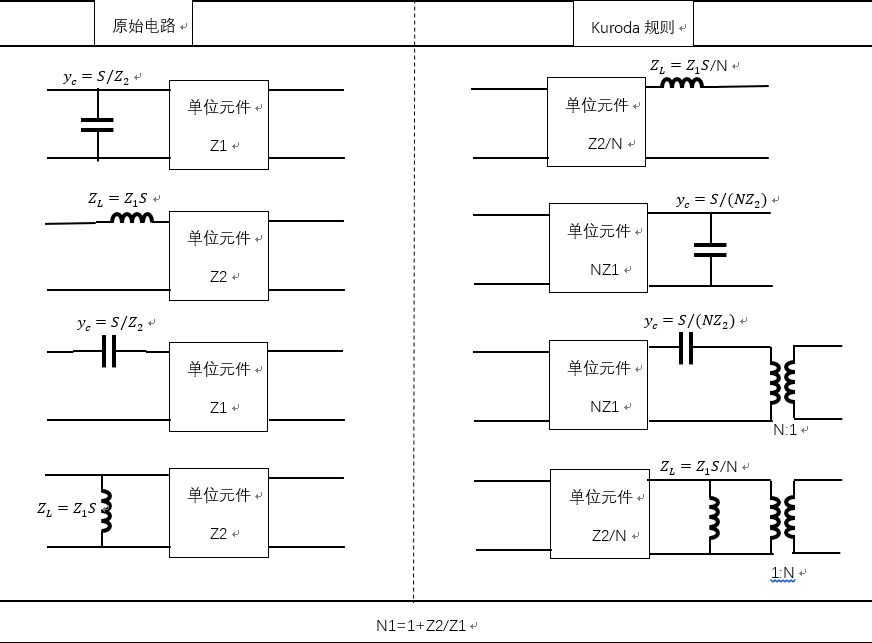
图5.3 科洛达规则