一、上节课知识点回顾
1)人工智能;大数据;机器学习;
2)上节课提到的打印水仙花数的程序(用4种方法实现)
所谓水仙花数是指1个3位的十进制数,其各位数字的立方和等于该数本身。例如:153是水仙花数,因为
水仙花数只是自幂数的一种;自幂数是指一个 n 位数,它的每个位上的数字的 n 次幂之和等于它本身。
二、朴素贝叶斯算法(Naive Bayesian)
拉普拉斯: 概率论只不过是把常识用数学公式表达了出来。
1) 贝叶斯方法: 正向概率;逆概问题
忘记了贝叶斯公式?推导一下。
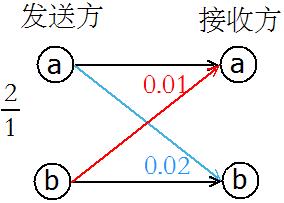
计算:
1) 接收方收到的信息是a的概率是多少?
2) 若接收方收到的信息是a,原发信息是a的概率是多少?
假设:
- D表示事件“将信息a传递出去”;
- R表示事件“接收到的信息是a”。
通过上面的例题,推导出贝叶斯公式,如下:
2) 垃圾邮件过滤
- 假设我的邮箱里有500封正常邮件(ham),200封垃圾邮件(spam),现在来了一封新邮件,我发现里面出现了单词discount,那么这封邮件是垃圾邮件的概率有多大呢?
- 我检查了一下所有邮件,发现垃圾邮件中包含单词discount的有50封,非垃圾邮件中包含单词discount的有20封。
- 然而,实际情况是,一封邮件通常包含了大量的单词,假设为 , 那么我们需要计算的是给定单词向量
, 这封邮件是垃圾邮件的概率是多少?
- 借助“朴素”之力。
3) 条件独立
在给定C的条件下,A和B条件独立当且仅当
P(AB|C) = P(A|C) * P(B|C) 或
P(A|BC) = P(A|C)
"朴素"之意实际上是独立性假设, 对于垃圾邮件过滤即认为每个单词的出现与否是条件独立的,因此
三、朴素贝叶斯优缺点
优点:
既简单又快速,在多类预测问题上表现良好;
当独立性假设成立时,朴素贝叶斯分类器与逻辑回归等其他模型相比表现更好,而且需要的训练数据也更少;
相较于数值变量,朴素贝叶斯分类器更适合解决分类变量问题。若是数值变量,需要满足正态分布。
缺点:
朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进;
需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致预测效果不佳;
由于我们是通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率。
对输入数据的表达形式很敏感。
四、朴素贝叶斯的四种应用
实时预测:朴素贝叶斯是一个快速的学习分类器,因此适用于实时预测。
多类预测:朴素贝叶斯以多类别预测功能闻名,因此可以用来预测多类目标变量的概率。
文本分类/垃圾邮件过滤/情感分析:朴素贝叶斯分类器主要用于文本分类,相比其他算法具有更高的成功率。 因此,它被广泛用于垃圾邮件过滤和情感分析(在社交媒体分析中,识别用户的积极和消极情绪)。
推荐系统:朴素贝叶斯分类器和协作过滤共同构建推荐系统,并使用机器学习和数据挖掘技术过滤看不见的信息以及预测用户是否喜欢系统的推荐。
