授课题目：

计算机体系结构及其编码方式（二）

教学目标：

1.  掌握二进制及其运算特点，计算机采用二进制的原因以及二进制的运算方法；

2.  了解ASCII码字符集合，了解汉字在计算机中有多种编码；

3.  能够理解补码的作用。

教学重点：

   计算机的语言(机器语言)是二进制，数值数据和非数值数据都需要进行编码才能在计算机中存储和处理；数据的二进制表示特点和运算规则。

教学难点：

数据编码。

教学方式与教学安排：

讲授课   2学时

教学内容：

2.4. 计算机中的数值数据的表示

1．基本概念

在计算机内部表示二进制数的方法通常称为数值编码，把一个数及其符号在机器中的表示加以数值化，这样的数称为机器数。机器数所代表的数称为该机器数的真值。要完整地表示一个机器数，应考虑三个因素：机器数的范围；机器数的符号；机器数中小数点的位置。

（1）机器数的范围：由计算机的CPU字长来决定。

当使用8位寄存器时，字长为8位，所以一个无符号整数的最大值是：（11111111）B=（255）D，此时机器数的范围是0~255。

当使用16位寄存器时，字长为16位，所以一个无符号整数的最大值是：（1111111111111111）B=（FFFF）H=（65535）D，此时机器数的范围是0~65535。

（2）机器数的符号：在算术运算中，数据是有正有负的，称之为带符号数。为了在计算机中正确地表示带符号数，通常规定每个字长的最高位为符号位，并用“0”表示正数，用“1”表示负数。例如：字长为8位二进制时，D7为符号位，其余D6~D0为数值位；字长为16位二进制数时，D15为符号位，其余D14~D0为数值位。

  （3）机器数中小数点的位置：在机器中，小数点的位置通常有两种约定，一种规定小数点的位置固定不变，这时的机器数称为“定点数”；另一种规定小数点的位置可以浮动，这时的机器数称为“浮点数”。

2．带符号数的原码、反码、补码表示

（1）原码：规定正数的符号位为0，负数的符号位为1，其它位按照一般的方法来表示数的绝对值。用这样的表示方法得到的就是数的原码。

例如：当机器字长为8位二进制数时：

            X＝＋1011011           [X]原码＝01011011

            Y＝－1011011           [Y]原码＝11011011

原码表示的整数范围是－(2n-1－1)~ ＋(2n-1－1)，其中n为机器字长。

通常：8位二进制原码表示的整数范围是－127~＋127，

     16位二进制原码表示的整数范围是－32767~＋32767。

（2）反码：对于一个带符号的数来说，正数的反码与其原码相同，负数的反码为其原码除符号位以外的各位按位取反。

例如：当机器字长为8位二进制数时：

          X＝＋1011011     [X]原码＝01011011     [X]反码＝01011011

          Y＝－1011011     [Y]原码＝11011011     [Y]反码＝10100100

负数的反码与负数的原码有很大的区别，反码通常用作求补码过程中的中间形式。反码表示的整数范围与原码相同。

（3）补码：正数的补码与其原码相同，负数的补码为其反码在最低位加1。

例如：X＝＋1011011    [X]原码＝01011011  [X]补码＝01011011

      Y＝－1011011  [Y]原码＝11011011  [Y]反码＝10100100  [Y]补码＝10100101

补码表示的整数范围是－2n-1~＋（2n-1－1），其中n为机器字长。

则：8位二进制补码表示的整数范围是－128~＋127，

16位二进制补码表示的整数范围是－32768~＋32767。

（4）补码与真值之间的转换：给定机器数的真值可以通过补码的定义来完成真值到补码的转换，若已知某数的补码求其真值，计算方法如下：正数补码的真值等于补码的本身；负数补码转换为其真值时，将补码按位求反末位加1，即可得到该负数补码对应的真值。

【例】 给定 [X]补码＝01011001B，求真值X；给定[X]补码＝11011010B，求真值X。

（1）由于[X]补码代表的数是正数，则其真值：

X＝＋1011001B

＝＋（1×26＋1×24＋1×23＋1×20）

＝＋（64＋16＋8＋1）

＝＋（89）D

（2）由于[X]补码代表的数是负数，则其真值：

X＝－（[1011010]求反＋1）B

＝－（0100101＋1）B

＝－（0100110）B

＝－（1×25＋1×22＋1×21）

＝－（32＋4＋2）

＝－（38）D

浮点数的表示：浮点数是属于有理数中某特定子集的数的数字表示，在计算机中用以近似表示任意某个实数。具体的说，这个实数由一个整数或定点数（即尾数）乘以某个基数（计算机中通常是2）的整数次幂得到，这种表示方法类似于基数为10的科学计数法。

单精度格式: 32位, 阶码E=8位, 尾数M=23位

双精度格式: 64位, E=11位, M=52位

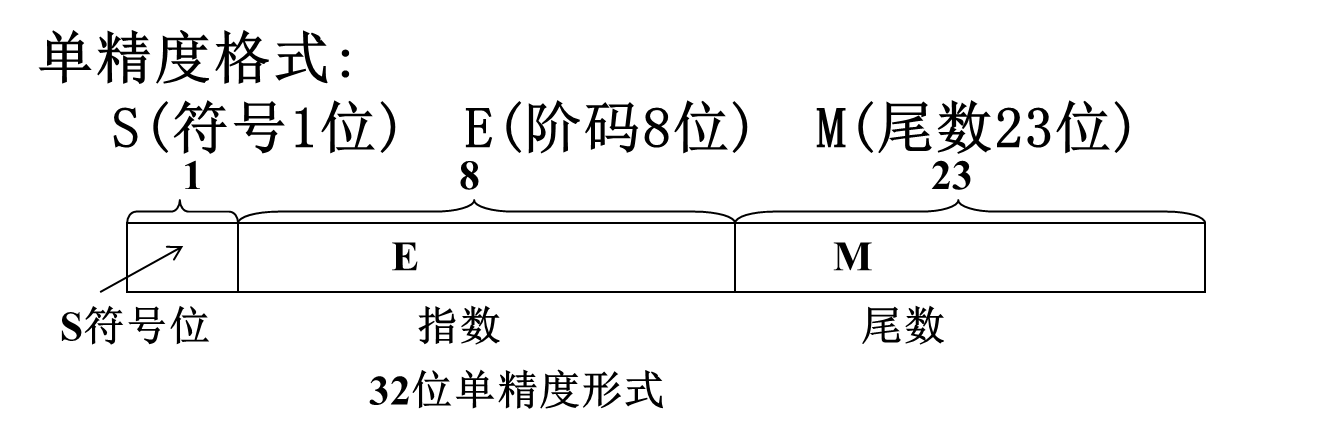
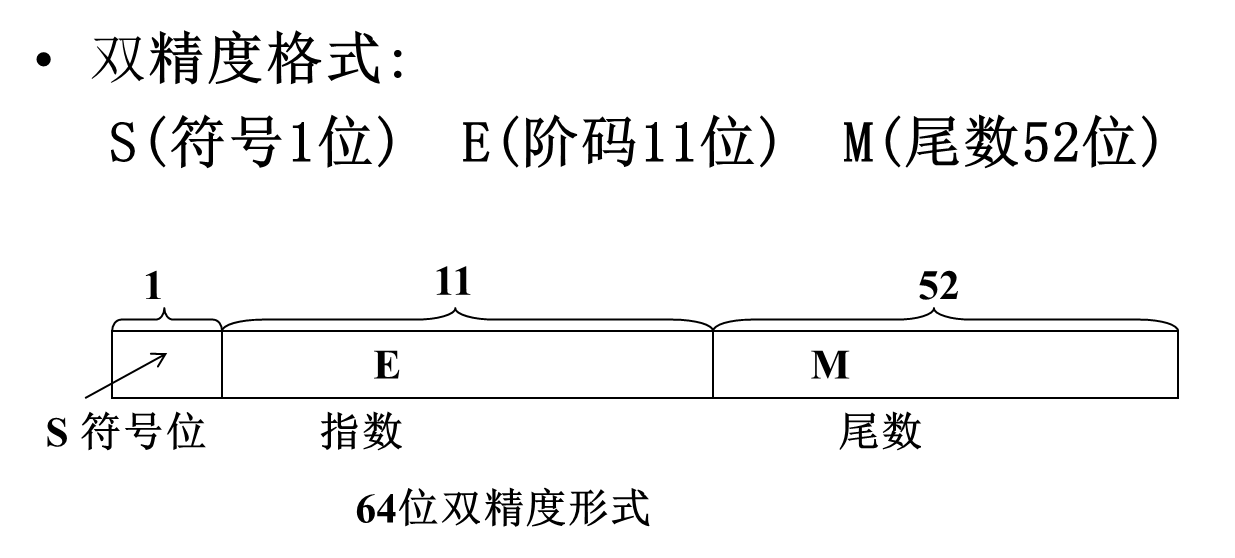
精度与范围

单精度格式表示范围：-3.4*10^38～3.4*10^38。

双精度格式表示范围：1.7x10^(-308) ~ 1.7x10^308。

2.5.计算机常用的编码

1．美国信息交换标准代码（ASCII码）

  ASCII（American Standard Code for InformationInterchange）码是美国信息交换标准代码的简称，用于给西文字符编码，包括英文字母的大小写、数字、专用字符、控制字符等。这种编码由7位二进制数组合而成，可以表示128种字符，

   ASCII码是7位二进制编码，而计算机的基本存储单位是字节（byte），一个字节包含8个二进制位（bit）。因此，ASCII码的机内码要在最高位补一个0。在存储、处理和传送信息时，最高位常用作奇偶校验位，用来检验代码在存储和传送过程中是否发生错误。奇校验时，每个代码的二进制形式中应有奇数个1；偶校验时，每个代码的二进制形式中应有偶数个1。

2．二—十进制编码——BCD码

  BCD（Binary-Coded  Decimal）码又称为“二—十进制编码”，专门解决用二进制数表示十进数的问题。

“二—十进制编码”最常用的是8421编码，其方法是用4位二进制数表示1位十进制数，自左至右每一位对应的位权是8、4、2、1。

由于4位二进制数有0000~1111共16种状态，而十进制数0~9只取0000~1001的10种状态，其余6种不用。

通常，BCD码有两种形式，即压缩BCD码和非压缩BCD码。

（1）压缩BCD码：压缩BCD码的每一位数采用4位二进制数来表示，即一个字节表示两位十进制数。例如：十进制数59D，采用压缩BCD码表示为二进制数是01011001B。

（2）非压缩BCD码：非压缩BCD码的每一位数采用8位二进制数来表示，即一个字节表示1位十进制数。而且只用每个字节的低4位来表示0~9，高4位为0。例如：十进制数87D，采用非压缩BCD码表示为二进制数是00001000 00000111B。

3．汉字编码

具有汉字信息处理能力的计算机系统，除了配备必要的汉字设备和接口外，还应该装配有支持汉字信息输入、输出和处理的操作系统。计算机处理汉字信息的前提条件是对每个汉字进行编码，这些编码统称为汉字代码。目前计算机中常用的几种汉字代码有：

（1）汉字输入码：用于外部输入汉字，也称为外码。它位于人机界面上，面向用户，其编码原则是简单易记、操作方便、有利于提高输入速度。目前使用较多的有顺序码——将汉字按一定顺序排好，然后逐个赋予1个号码作为该汉字的编码，例如区位码；音码——根据汉字的读音进行编码，例如拼音码；形码——根据汉字的字形进行编码，例如五笔字型；音形码——根据汉字的读音和字形进行编码，例如双拼码。

如下图就是两种字形码的表示方法，这样的字形信息便于缩放和变换，并且字形美观。

点阵字形码：记录每个点的黑白       

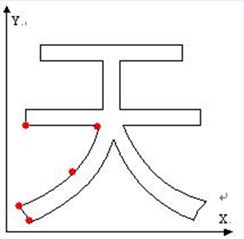
矢量字形码：记录各点坐标和它们的关系

（2）汉字机内码：是汉字处理系统内部存储、处理汉字而使用的编码，简称内码。内码与国家标准GB2312-80汉字字符集有简明的一一对应关系。

（3）汉字交换码：是汉字信息处理系统之间或通信系统之间传输信息时，对每个汉字所规定的统一编码。我国已指定了汉字交换码的国家标准“信息交换用汉字编码字符集——基本集”，代号GB2321-80，又称“国标码”。

该字符集的内容由三部分组成：

第一部分是各类符号、各类数字以及各种字母、包括英文、俄文、罗马字母、日文平假名与片假名、拼音符号和制表字符，共687个，第二部分为常用汉字，有3755个汉字，通常占常用汉字的90%左右，按拼音字母顺序排列，以便于查找。第三部分为二级常用汉字，有3008个，按部首顺序排列。