授课题目：

计算机体系结构及其编码方式（一）

教学目标：

1.  了解图灵机模型的构成和计算过程；

2.  了解计算的过程可以被分解成一系列非常简单的动作；

3.  掌握冯·诺依曼原理；

4.  掌握二进制及其运算特点，计算机采用二进制的原因以及二进制的运算方法；

教学重点：

    冯·诺依曼计算机的“存储程序、程序控制”概念；计算机的基本构成；计算过程可以被分解为一系列非常简单的动作；计算机的语言(机器语言)是二进制。

教学难点：

图灵机模型的认识，程序的概念，数据编码。

教学方式与教学安排：

讲授课   2学时

作业及课外学习要求：

练习不同进制数据编码表示方法，转换方法和运算规则。

可参考线上图书：

教学内容：

2 计算机体系结构及其编码方式

  本章的主要内容

（1）如何使机器具有计算能力？

（2）图灵机与冯.诺依曼原理（重点）

（3）二进制的产生和运算（重点）

（4）  数的表示：数据的编码的基本原理（难点）

2.1.机器的计算能力与图灵机

用机器来模拟人们用纸笔进行数学运算的过程，他把这样的过程看作下列两种简单的动作：

1. 1.在纸上写上或擦除某个符号；

2. 2.把注意力从纸的一个位置移动到另一个位置；

而在每个阶段，人要决定下一步的动作，依赖于 (a) 此人当前所关注的纸上某个位置的符号和（b) 此人当前思维的状态。

为了模拟人的这种运算过程，图灵构造出一台假想的机器，该机器由以下几个部分组成：

1. 1.一条无限长的纸带 TAPE。纸带被划分为一个接一个的小格子，每个格子上包含一个来自有限字母表的符号，字母表中有一个特殊的符号表示空白。纸带上的格子从左到右依此被编号为 0,1,2,... ，纸带的右端可以无限伸展。

2. 2.一个读写头 HEAD。该读写头可以在纸带上左右移动，它能读出当前所指的格子上的符号，并能改变当前格子上的符号。

3. 3.一套控制规则 TABLE。它根据当前机器所处的状态以及当前读写头所指的格子上的符号来确定读写头下一步的动作，并改变状态寄存器的值，令机器进入一个新的状态。

4. 4.一个状态寄存器。它用来保存图灵机当前所处的状态。图灵机的所有可能状态的数目是有限的，并且有一个特殊的状态，称为停机状态。参见停机问题。

注意这个机器的每一部分都是有限的，但它有一个潜在的无限长的纸带，因此这种机器只是一个理想的设备。图灵认为这样的一台机器就能模拟人类所能进行的任何计算过程。

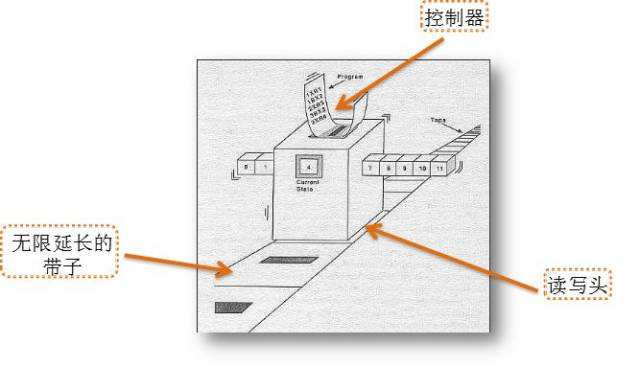
• 图灵机，又称图灵计算、图灵计算机，是由数学家艾伦·麦席森·图灵（1912～1954）提出的一种抽象计算模型，即将人们使用纸笔进行数学运算的过程进行抽象，由一个虚拟的机器替代人们进行数学运算。

所谓的图灵机就是指一个抽象的机器，它有一条无限长的纸带，纸带分成了一个一个的小方格，每个方格有不同的颜色。有一个机器头在纸带上移来移去。机器头有一组内部状态，还有一些固定的程序。在每个时刻，机器头都要从当前纸带上读入一个方格信息，然后结合自己的内部状态查找程序表，根据程序输出信息到纸带方格上，并转换自己的内部状态，然后进行移动。

计算的过程可以被分解成一系列非常简单的动作。

2.2.冯·诺依曼原理

从20世纪初，物理学和电子学科学家们就在争论制造可以进行数值计算的机器应该采用什么样的结构。人们被十进制这个人类习惯的计数方法所困扰。所以，那时以研制模拟计算机的呼声更为响亮和有力。20世纪30年代中期，美籍科学家冯诺依曼大胆的提出，抛弃十进制，采用二进制作为数字计算机的数制基础。同时，他还说预先编制计算程序，然后由计算机来按照人们事前制定的计算顺序来执行数值计算工作。

冯诺依曼理论的要点是：数字计算机的数制采用二进制；计算机应该按照程序顺序执行。

人们把冯诺依曼的这个理论称为冯诺依曼体系结构。从EDVAC到当前最先进的计算机都采用的是冯诺依曼体系结构。所以冯诺依曼是当之无愧的数字计算机之父。

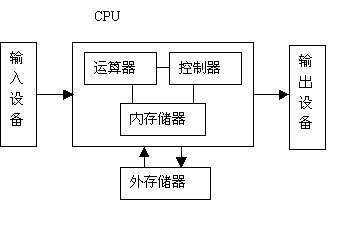
根据冯诺依曼体系结构构成的计算机，必须具有如下功能：

把需要的程序和数据送至计算机中。

必须具有长期记忆程序、数据、中间结果及最终运算结果的能力。

能够完成各种算术、逻辑运算和数据传送等数据加工处理的能力。

能够根据需要来控制程序走向，并能根据指令来控制机器的各部件协调操作。

能够按照要求将处理结果输出给用户。

为了完成上述功能，计算机必须具备五大基本组成部件，包括：

1. 1.输入数据和程序的输入设备-输入设备

2. 2.记忆程序和数据的存储器-存储器

3. 3.完成数据加工处理的运算器-运算器

4. 4.控制程序执行的控制器-控制器

5. 5.输出处理结果的输出设备-输出设备

2.3.二进制的产生

二进制是德国数学家莱布尼茨于1700年发明的，他提出了用二进制表示所有自然数的一张表。对于当时的数学家来说，这不过是一种数字游戏。

然而由于冯·诺依曼原理，采用二进制表示数据成为现代计算机的通用方法，才使得二进制表示方法重要了起来。

巧合的是，中国古代的易经的八卦图，也采用了二进制的形式，莱布尼茨也曾经表示过对易经的兴趣，由此还产生了莱布尼茨受易经启发而发明二进制的讹传。

计算机就其本身来说是一个电器设备,为了能够快速存储、处理、传递信息,其内部采用了大量的电子元件,在这些电子元件中,电路的通和断、电压高低,这两种状态最容易实现,也最稳定、也最容易实现对电路本身的控制。我们将计算机所能表示这样的状态,用0,1来表示、即用二进制数表示计算机内部的所有运算和操作。

各种进制：

2、8、10、12、16、60、360

都是为了计数和运算方便而约定的记数系统。

R进制的概念——满R进1，借1当R

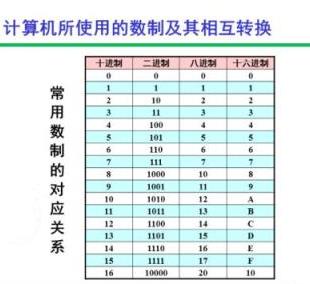
二进制与其他进制的转换

首先我们得了解一个概念，叫“权”。“权”就是进制的基底的n次幂。如二进制的权就是（2）*n了，十进制的权就是（10）*n，看到十进制我们就很自然的想到科学计算法中的（10）*n，对吧？有了权这个定义之后，我们就可以随便把一个进制的数转化成另一个进制的数了。日常生活中，由于电脑的字节，汉字西文的字节的原因，二进制最常见的转换是八进制，十六进制，三十二进制，当然还有十进制。

二进制转换成十进制的原则是：基数乘以权，然后相加，简化运算时可以把数位数是0的项不写出来，（因为0乘以其他不为0的数都是0）。小数部分也一样，但精确度较少。

二进制与八进制的转换：采用“三位一并法”（是以小数点为中心向左右两边以每三位分组，不足的补上0）这样就可以轻松的进行转换。

二进制与十六进制的转换：采用的是“四位一并法”，就如二进制与八进制的转换一样。

二进制的算术运算

   运算二进制的加法：0+0=0，0+1=1，1+0=1， 1+1=10(向高位进位)；即7=111

10=1010 3=11

　运算二进制的减法：0-0=0，0-1=1(向高位借位) 1-0=1，1-1=0(模二加运算或异或运算) ；

　运算二进制的乘法：0 * 0 = 0　0 * 1 = 0，1 * 0 = 0，1* 1 = 1 二进制的除法：0÷0 = 0，0÷1 = 0，1÷0 = 0 (无意义)，1÷1 = 1 ；

　逻辑运算二进制的或运算：遇1得1 二进制的与运算：遇0得0 二进制的非运算：各位取反。