“模糊数学”教学大纲

 课程编号: MS006021                      

课程名称:模糊数学                              英文名称：Fuzzy Mathematics

学分/学时：1/16                               课程性质：选修

适用专业:理工类专业                            建议开设学期：第1学期

先修课程:                                  开课单位：数学与统计学院

一、课程教学目标与任务

模糊数学是理工类专业的一门选修课。模糊数学是运用数学方法研究和处理模糊性现象的一门数学新分支，它以“模糊集合”论为基础，打破了以二值逻辑为基础的传统思维，使模糊推理成为严格的数学方法.在模式识别、人工智能等方面有着广泛的应用。通过本课程的学习，使学生掌握模糊数学的基本理论知识和基本思维方法，增强培养学生分析问题解决问题的能力，提高学生的创新精神和应用数学的能力。

二、课程的具体内容及基本要求

本课程简明阐述了模糊数学的基本理论和基本方法，主要介绍模糊集与运算、分解定理与表现定理及其在科学技术领域的应用：模糊模式识别、模糊关系与模糊综合评价、模糊聚类分析、模糊线性规划和模糊控制。

第一章、模糊集的基本概念（4学时）

教学内容: （1）模糊数学概述 （2）模糊理论的数学基础 （3）模糊子集及运算 （4）模糊集的基本定理

1.基本要求:

（1）熟练掌握模糊集合的概念与模糊集合的运算及其运算性质；

（2）理解经典的扩张原理及二元关系；

（3）掌握模糊集截集的概念及其性质，理解模糊集的分解定理及扩张原理；

（4）了解隶属函数的确定及模糊集的应用。

2.重点与难点:模糊集概念及其计算、模糊集截集、分解定理及扩张原理。

  采用的教学方法及要求：课堂讲授、讨论。

3.作业及课外学习要求：完成作业和自学内容。

第二章模糊聚类分析（4学时）

教学内容:（1）模糊矩阵 （2）模糊关系 （3）模糊等价矩阵（4）模糊聚类分析及其应用

1.基本要求

（1）熟练掌握模糊矩阵的概念与模糊矩阵的运算及其运算性质；

（2）熟练掌握模糊矩阵传递闭包的定义及性质，理解模糊矩阵的基本定理；

（3）掌握模糊关系的定义及模糊关系的运算与性质；

（4）掌握两种特殊的模糊关系：模糊相似关系与模糊等价关系；     

（5）掌握模糊聚类分析的方法与步骤。

2.重点与难点:模糊关系与模糊矩阵、模糊关系的合成、模糊等价、相似关系，传递闭包的求解。

  采用的教学方法及要求：课堂讲授、讨论。

3.作业及课外学习要求：完成作业和自学内容。

第三章模糊模型识别（2学时）

 教学内容:（1）模糊模型识别简介 （2）第一类模糊模型识别 （3）第二类模糊模型识别（4）贴近度的改进及模糊模型识别的应用

 1.基本要求:

（1）理解模糊模型识别的定义；

（2）熟练掌握第一类模糊模型识别的方法：最大隶属原则Ⅰ及最大隶属原则Ⅱ；

（3）熟练掌握第二类模糊模型识别的方法：择近原则及多属性的择近原则；

（4）了解贴近度的改进方法及模糊模型识别的应用。

 2.重点与难点:最大隶属原则、择近原则的方法、两类模糊模型识别的方法。

   采用的教学方法及要求：课堂讲授、讨论。

 3.作业及课外学习要求：完成作业和自学内容。

第四章、模糊决策（2学时）

教学内容:（1）模糊意见集中决策 （2）模糊二元对比决策 （3）模糊综合评判决策

1.基本要求:

（1）掌握模糊意见集中决策的方法；

（2）掌握模糊二元对比决策的方法；

（3）了解模糊综合评判决策。

2.重点与难点:模糊意见集中决策、模糊二元对比决策、模糊综合评判决策的基本方法与步骤。

  采用的教学方法及要求：课堂讲授、讨论。

3.作业及课外学习要求：完成作业和自学内容。

第五章、模糊线性规划（2学时）

教学内容:（1）线性规划模型简介 （2）模糊环境下的条件极值 （3）模糊线性规划模型

1.基本要求:

（1）了解模糊环境下条件极值的求解方法；

（2）了解几种特殊的模糊线性规划及其求解.

2.重点与难点:模糊规划模型及其求解。

  采用的教学方法及要求：课堂讲授、讨论。

3.作业及课外学习要求：完成作业和自学内容。

第六章、模糊控制（2学时）

教学内容:（1）现代控制系统简介 （2）模糊控制器

1.基本要求:

 初步了解模糊控制原理及简单模糊控制器的设计原理及方法。

2.重点与难点:模糊控制原理与简单模糊控制器的设计原理及方法。

  采用的教学方法及要求：课堂讲授、讨论。

3.作业及课外学习要求：完成作业和自学内容。

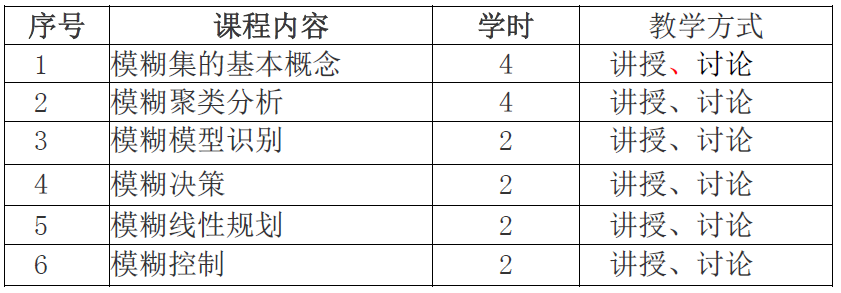
 三、教学内容与学时安排

总学时16学时，其中：讲授14学时，实验 0 学时，上机 0 学时，实践 0 学时，研讨 2 学时，线上 0 学时。

四、本课程对培养学生能力和素质的贡献点

    本课程主要介绍了利用模糊数学的知识来解决实际问题的理论和方法。通过本课程的学习，使学生掌握模糊数学有关方面的理论知识和处理模糊现象的基本思维方法，培养学生具有抽象概括问题的能力、逻辑推理能力、运算能力和综合运用所学知识分析问题、论证问题和解决问题的能力，为学生的后继学习以及将来从事科学研究与技术创新等工作奠定必要的数学基础。

五、考核及成绩评定方式

总评成绩由平时成绩和期末课程论文成绩按比例综合而成.各部分所占比例如下：

平时成绩： 60%。包括平时作业（上机实验）和课堂考勤等.平时作业主要考核对课堂学习知识点的理解和掌握程度。

课程论文成绩：40%.主要考核发现、分析和解决问题的能力，语言及文字表达能力。.

过程成绩提交时间和总评成绩计算说明表

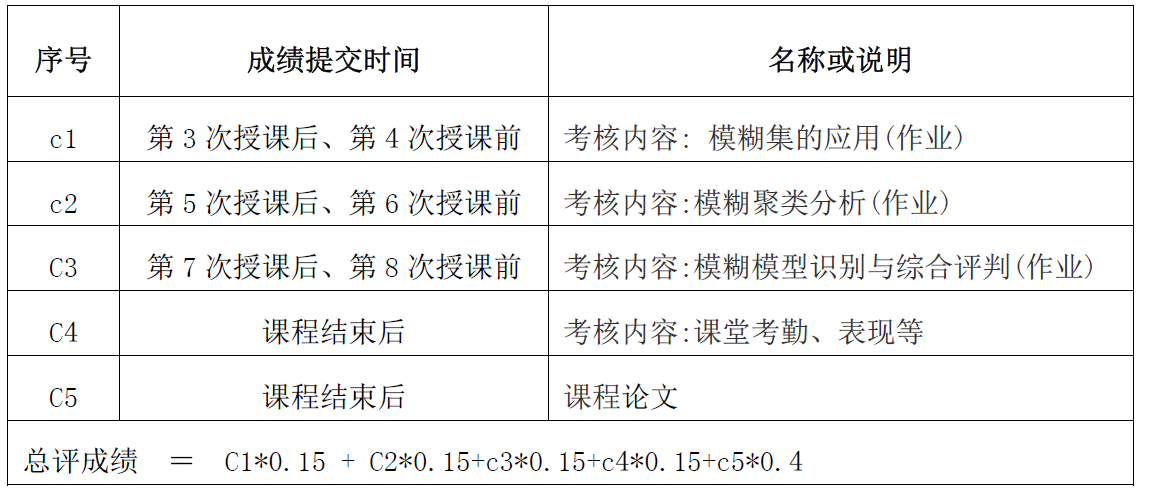
注：上表用于说明授课过程中分项成绩提交时间，教师应在规定的时间内提交对应成绩，提前或逾期无法提交，一旦提交无法修改。大纲可以根据需要自行定义提交成绩的次数、时间和名称或说明，总评成绩计算必须与考核和成绩评定方式中描述的一致。

六、 教材及参考书目

  教 材：

谢季坚.模糊数学及其应用(第三版).武汉:华中理工大学出版社.2006.8

  参考书目：

1.韩立岩，汪培庄.应用模糊数学.首都经济贸易大学出版社.1998.1

2.张国立，张辉，孔倩. 模糊数学基础及应用. 化学工业出版社.2011.

3.张振良编.应用模糊数学.重庆大学出版社.1991.

4.高英仪，凌卫新.模糊数学原理及应用.华南理工大学出版社.2011.

5.刘林.应用模糊数学.陕西科学技术出版社.2008.2 

                                 ( 执笔人:张剑湖   审核人:韩邦合)

                                              2018年8月